量子點和表面等離激元相互作用可以形成束縛态,此時,處于激發态的量子點不會完全衰減到基态,而是演化到此束縛态上。最近,3044永利集团的黃勇剛教授與王小雲教授合作指導碩士研究生文莎莎,提出了一套系統的數值研究方法,能快速确定束縛态的形成條件以及獲得量子點的非馬爾科夫自發輻射動力學。相關文章發表于Optics Express 28(5):6469-6489(2020)。
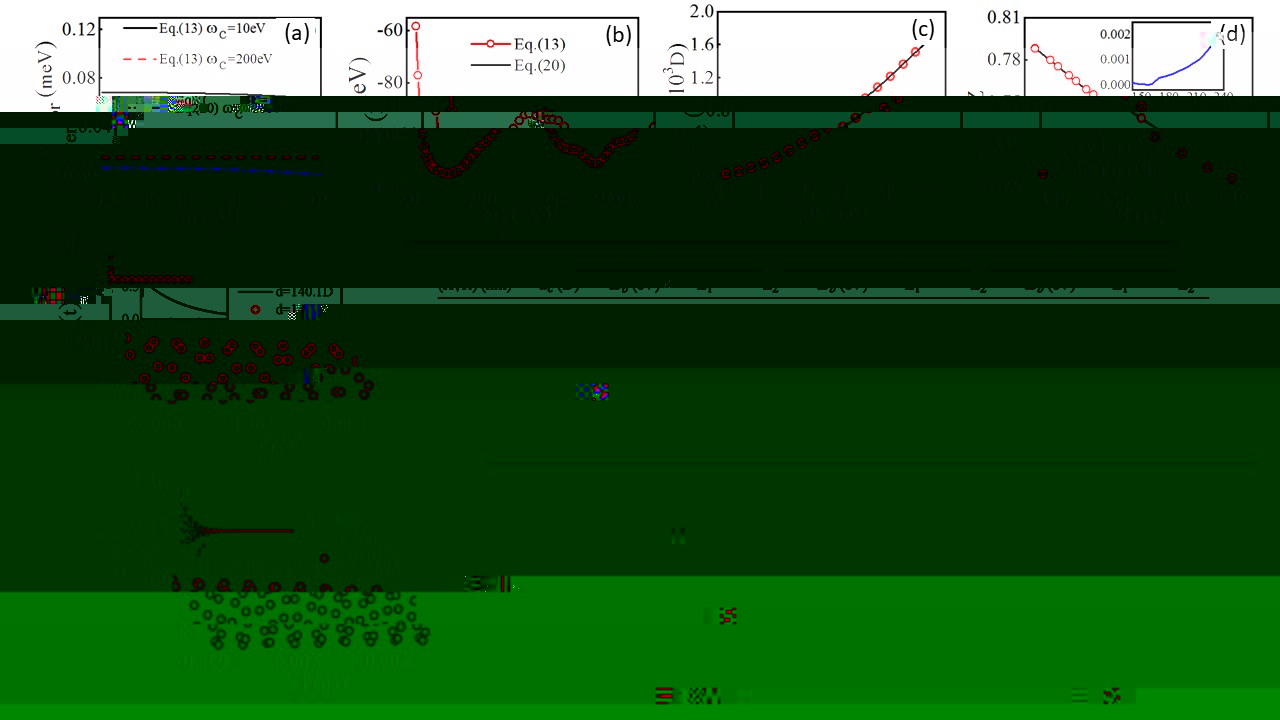
具體的,确定系統是否存在束縛态隻需計算微納結構中量子點處的0頻光子散射格林函數(見公式25)。當系統存在束縛态時,我們提供了一種無需束縛态本征頻率即可快速求解穩态時量子點處于激發态的幾率(見公式24)。此外,我們推廣了課題組之前所發展的快速準确計算能級移動的方法(Physical Review A 99(5), 053844 (2019)),發現了負頻率時的能級移動與正頻時能級移動的非共振項之間的相等關系(見公式20),相比于通用的方法(見公式13),該方法計算結果準确,收斂快(見圖2和圖7)。利用該結果,我們可快速準确獲得束縛态的本征頻率(公式21的零點)。利用所得的能級移動和束縛态共振頻率,我們發現格林函數預解算子方法能快速準确求解系統的動力學,且系統的非馬爾科夫動力學可通過公式26解釋為非共振幹涉。
該工作得到了國家自然科學基金(11564013, 11964010, 11564012, 11464014, 11464013)和湖南省研究生創新基金(CX2018B706, CX20190876)的支持。
[1] Sha-Sha Wen, Yong-Gang Huang*, Xiao-Yun Wang*, Jie Liu, Yun Li, Xiu-E Quan, Hong Yang, Jin-Zhang Peng, Ke Deng, and He-Ping Zhao, Opt.Express 28(5)(2020).
https://www.osapublishing.org/oe/abstract.cfm?uri=oe-28-5-6469&origin=search#figanchor2